Constructivism and Mathematics
Mathematical language is used to abstract phenomena and to translate the different levels of abstraction across different domains. This seemingly innocent sentence could spark some controversy among practitioners. Many interpret the field platonically, that is, they understand the practising mathematician as uncovering the mysteries of objects and structures which exist on some abstract domains but bear only an inexact, approximate correspondence with the real objects constituting our experience of nature and the world.
A different case is the one offered by the more modern categorical perspective. Category theory is a branch of mathematics where the emphasis shifts from objects themselves to the relationships (called morphisms) between them. Ideal mathematical objects are shifted into the background: what really matters is instead the relationship between them; their essential properties are reflected in the way different objects can be mapped to each other preserving their defining structure. Objects in a category have a weaker reliance on their complete syntactic definition. Category theory shifts the emphasis from the internal syntax of objects (how they are presented, what they are ‘made of’) to their external behaviour as captured by morphisms.
Let me give a concrete example. When we are introduced to group theory in a first-year algebra course we start by saying that a group is a “set”—a collection of “elements”—equipped with an operation combining two elements into a third one, subject to rules such as associativity, the existence of an identity element, and the existence of inverses. The definition of these objects is very general, but it turns out that they are ubiquitous and useful mathematical objects. They are used, for example, to modelling physical symmetries, to describe rotations and motions, and to account for molecular symmetries.
But what do we do when we use a mathematical structure to model, say, a physical phenomenon? When we use group theory to model, say, the symmetry of a physical object, we are describing a “map” to such an ideal platonic structure, and we use the existence of these maps to provide bridges between different phenomena united by the existence of this “analogy.” The world of pure mathematical forms provides a formal bridge between objects that are concrete and, in their complexity, do not fully conform to the ideal mathematical emanation.
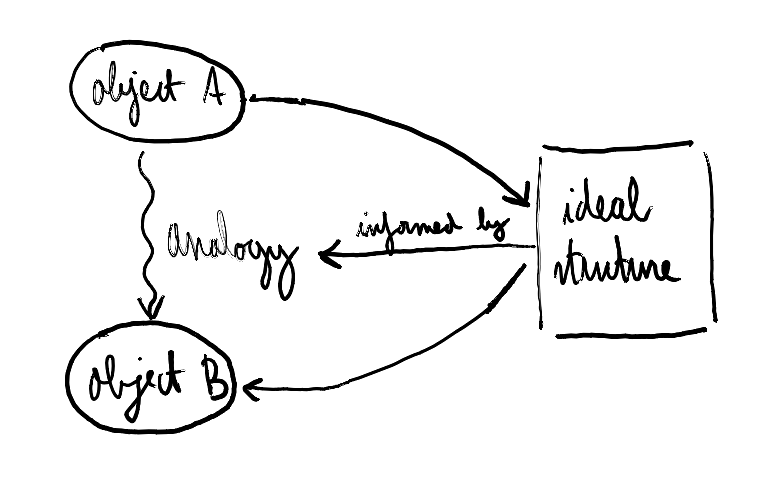
There is here a fundamental problem: concrete features are united by making use of this ideal platonic world of forms, while it is this world itself which is synthesised by our experiences. We have constructed a pure layer of abstraction which does not conform exactly to any of the forms that it was meant to describe in the first place, it will never do so if the foundation of mathematics remains syntactic. Category theory resolves this by moving the focus onto the existence of the maps between these objects. The notion of analogy can be reinstated and reinterpreted without making use of platonic abstraction. In a way, category theory demystifies the fact that the mathematical structures that were identified in the course of the formulation of mathematical theories as we know them are abstractions of analogies, the recognition of patterns that are ubiquitous in our phenomenological understanding.
Surely this does not a priori rule out the possibility of a world of pure form where the interaction of these forms is seamless, but it relaxes the need for such a platonic world of forms in the first place.
In short, the forms studied by mathematics in their aseptic beauty are actually tools that interpret the existence of certain types of relationships between a variety of scattered domains. Group theory, for example, as any other specific mathematical theory describes a grammar of analogies between forms that modern mathematics has reified.
Sheaf Happens
We might think that what we have talked about so far has little relationship with the main topic of this blog post. I believe it is necessary to understand the perspective from which sheaf theory, but specifically applied categorical methods, distinguish themselves from other more classical (in the historical sense) mathematical approaches.
This summer NeverLocal participated in a workshop on the application of the theory of sheaves at Bochum University, which ran in the context of ESSLLI (The European Summer School on Logic and Information). We were invited as our research on the phenomenon of contextuality—what is used to certify the fundamental randomness arising from quantum mechanical experiments—can be naturally interpreted by making use of sheaf-theoretic language.
What is sheaf theory? Roughly speaking, it is a mathematical framework that tells us how local pieces of data can be consistently “glued” together to form global data. One of the cases where the formalism underpinning it results totally obscure and artificial to anyone not in the field, is nevertheless a type of situation that is ubiquitous and understandable. Suppose that you are reading a text: a single sentence has a “space” of possible meanings that becomes narrower once we take into consideration a bigger family of sentences which contains it. The meaning of a word specialises with the context.
On the other hand, not all the parts of a sentence or text possess meaning by themselves: it is not guaranteed that an arbitrary selection of non-adjacent words retains any form of meaning and, in particular, that this meaning has anything to do with the rest of the text. We need a formalism that describes this constructivist approach to meaning which is assigned dynamically to different parts of the text.
Usually, when we talk about spaces, the first mathematical idealisation that can come to mind is topology. A topology on a set is a way of specifying which subsets are “open,” where “open” means that a point can move around within them without crossing a boundary. To define the topology of a set of points you describe which sets can be thought of as being boundary-less.
Topology allows one to construct a notion of “closeness” which is weaker than the one implied by a metric structure, a quantitative description of the distance between any two points in the space. Any topological space gives a notion of restriction, tells us how to carve from the whole (which is always open by definition) sets without boundaries.
And here boundary is always a relative notion: the space itself is always open because there are no points “outside” and therefore no meaningful boundary to be defined. This may seem counterintuitive as we are often picturing or imagining topological spaces as “closed objects” immersed in some Euclidean environment. The reality is that the notion of “openness” is always relative, it has little to do with the points themselves but depends on the global structure of the topological space.
A presheaf is a construction that assigns a collection of local “data” to any open set of a topological space, with the requirement that the data be compatible with restriction to smaller open sets. If we take data assigned to an open set and restrict it to some proper (open) subset there must be a function mapping data defined on the bigger set onto the smaller one, a recipe for marginalising data defined on a bigger set. This allows to track data defined globally to some local region of the space.

The restriction functions guarantee that to every “global” assignment one can univocally assign the compatible “local” data. Passing from local to global is generally not fully determined, there might be several global assignments of data which give rise to the same local behaviour. If we require all the restriction maps to be bijections then we are describing a “constant presheaf,” a constant assignment of data which effectively does not see the topology of the underlying space, data assignment is completely agnostic to the topological structure.
There are particular types of presheaves which are called sheaves. These represent situations where the “global” can be univocally reconstructed from the local sections. A presheaf can fail to be a sheaf due to two possible failures of this univocality. There might be cases where there are multiple global behaviours that marginalise to the given local assignments (the ambiguity of gluing), or situations where such a gluing does not exist (the obstruction of gluing).
This simple idea, to have a mathematical language formalising how local assignments can be translated to global assignments and its possible failures, constitutes a very powerful technique: the field of sheaf theory provides a vocabulary and a substantial theoretical body of theorems and techniques that allows us, first of all, to give a name to phenomena and, moreover, to create equivalences and relationships between these terms, unveiling structures in a variety of cases where the dialogue between a local description and a global description becomes essential.
Bundle Up: It’s Quantum Mechanics
In quantum mechanics one of the defining conflicts is precisely the relationship between the local and the global. Let’s start with classical mechanics, the set of rules describing the principles of motion: it provides an account of how the working parts of nature interact and affect each other to describe the observable classical physical phenomena. In its foundations there is no space for stochasticity. Any probabilistic behaviour is only apparent: uncertainty is a consequence of the fact that the model chosen may not be adequate, that some parts of the mechanism will still be evident but there is somewhere a coarse-graining (a smoothing or averaging out of fine details) of the mechanical parts at play that obscures the true deterministic behaviour.
Often such a coarse-graining is important and can reveal phenomena that, due to their complexity, would be too difficult to account for by a classical-mechanical explanation—this is, for example, the case for statistical mechanics, the study of large systems where the collective behaviour emerges from averaging over countless microscopic states.
Quantum mechanics is said to be non-classical, but what is really non-classical about it? The formalism and the mechanical equations are certainly different, but can we pinpoint the assumption that is so inestricably interconnected with classical theories that it constitutes the obstacle to describing the phenomena in the microscopic regime of validity of quantum mechanics?
In the classical viewpoint one feels legitimate to eliminate the observer. What is observation? First of all it is the act of preparing a context for the synthesis of phenomena, the conditions, and the set-up that must be met before the experiment can be validly execute. But—and here one may understand the crucial importance of the sheaf-theoretic language—we are convinced, by practice, that even if there are different ways to prepare the observation which do not involve any fundamental incompatibility then we are entitled to regard them as compatible. The two local descriptions, each tied to its own way of preparing the experiment, can be glued together into a single global account where both conditions are verified at once. The sheaf condition assures us that such gluing is legitimate whenever the contexts overlap consistently: what seemed to be two distinct vantage points are in fact stitched together into a unified fabric of description.
Consider, for instance, the case of classical optics. One might prepare an experiment to study light as a wave—setting up interference fringes with a double slit—or, alternatively, describe it in terms of ray optics, tracing straight-line propagation through lenses and mirrors. These are two local descriptions, each adapted to a specific experimental context. Yet they are not fundamentally incompatible: both can be glued into the global description furnished by Maxwell’s equations, where wave and ray are revealed as approximations of a common underlying theory. This is precisely the sheaf-like move: local perspectives merge into a coherent global whole when their conditions can be satisfied together.
Even if to describe some behaviour we are nevertheless forced to consider an enlarged domain which includes the set-up, this can safely coexist with any other way to expose the mechanism experimentally; we therefore just get rid of it and can affirm the irrelevance of the observer.
This is crucial even in cases where the measurement does seem to be fundamentally imprecise. It is common in popular literature to reduce the problem of quantum mechanics to a fundamental inability to perform the measurement. This is not entirely true. Of course, it is reasonable to believe that a measurement of position will never be made with perfect precision, and of course different “contexts,” different measurement apparatus, will reveal different readings. Nevertheless, inscribed in the classical perspective is the belief that such a limiting value exists, even though in practice there will always be some—possibly context-dependent—experimental error. The impossibility of measuring simultaneously the position and the momentum of a particle in quantum theory is not merely a practical impossibility, it is the realisation that the quantum state of a system when measured with respect to these two different contexts showcases complementary phenomena—outcomes that cannot be unified into a single classical picture.
The statistical behaviour that, for example, appears in statistical mechanics—a non-deterministic theory—does not showcase this dependence on context. It can be seen as an assignment of statistical responses to experimental conditioning which nevertheless does satisfy the sheaf condition. This might seem a mathematical coincidence until it is realised that this is equivalent to postulating the existence of a deterministic mechanism attached to each context, obscured by the action of coarse-graining that characterises the statistical nature of the theory.
The application of sheaves to quantum theory began with the works of Samson Abramsky and collaborators. We have extended Abramsky’s approach by using the framework to analyse scenarios with arbitrary causal structures. This allows us to formally identify where and how fundamental randomness is used, and the extent to which it can be certified in a cryptographic protocol. We believe that the sheaf-theoretic framework offers the most precise characterisation of contextuality, and that its usefulness extends beyond the foundational or philosophical perspective sketched earlier in this blog post. This language can therefore be employed to formalise the cryptographic security of protocols, which relies on the ability to verify the fundamental randomness arising from the theory. For the readers interested in the formal underlying the sheaf theoretic approach to quantum protocols my slides available at the webpage of the workshop.
The formal language of sheaf theory is expressed in categorical terms, and for this reason it is particularly well suited to the kind of mathematical modelling we described earlier, well beyond the modelling of quantum correlations. At the ESSLLI 2025 workshop “Theory and Applications of Sheaf Theory,” the framework was presented as a way of layering a topological structure with data assignments, sometimes enriched with numerical information such as probabilities. This gives rise to a computational model that can bring together syntax, semantics, and statistics within a single framework. Because it allows one to define and compare both local and global measures—for instance, computing the difference between interpretations across contexts—it provides a useful perspective on how partial descriptions can combine into a whole, and how ambiguity or coherence spreads across levels of description. Originally developed to connect disparate areas of mathematics, such as differential equations and logic, sheaf theory has increasingly been applied to modelling experimental data across varied contexts: structural and statistical, analytic and empirical, linguistic and symbolic.
What stood out at the workshop was the wide range of communities making use of this framework: engineers applying sheaves in signal processing and robotics, researchers analysing quantum contextuality, cognitive scientists and psycholinguists studying human behaviour, analysts modelling social networks, and even computer scientists investigating coherence and reasoning in large language models. The event was not only a technical exchange but also a meeting point for researchers who see in the local-to-global structure of sheaves a common language that can be adapted across disciplines.