In this post, we introduce some of the fundamental ideas behind contextual cryptography, the use of quantum contextuality as a cryptographic resource.
- Conceptually, contextuality can be defined as the physical impossibility to fully predict the outputs of a random process, subject to free input choices made by the parties involved.
- Practically, contextuality is a way to generate intrinsically secure correlated randomness across multiple parties, randomness which is then used to power cryptographic protocols.
To get a concrete feel for how this works, we turn our attention to one of the simplest and better known example of this phenomenon, namely Bell’s experiment.
Bell’s Experiment
Two parties — call them Alice and Bob — each have one of two qubits in an entangled state $\vert\Phi^+\rangle$, as shown by the following circuit:
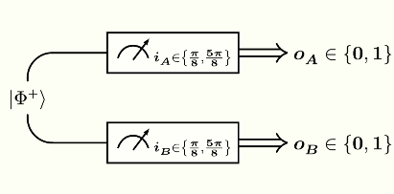
Alice and Bob are free to measure their qubits in one of two possible bases, defined by axes at angles of $\frac{\pi}{8}$ and $\frac{5\pi}{8}$ from the $\vert+\rangle$ state along the Bloch sphere’s equator:
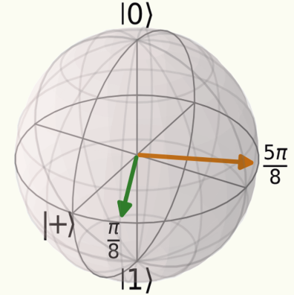
The inputs for this protocol are the measurement choices: they are binary, taking values $i_A, i_B \in \lbrace\frac{\pi}{8}, \frac{5\pi}{8}\rbrace$. The outputs for this protocol are the measurement outcomes: they are also binary, taking values $o_A, o_B \in \lbrace 0, 1\rbrace$ by convention.
Alice and Bob measure their qubits simultaneously, by flipping a random coin each to select their input. In fact, simultaneity is not strictly necessary: it is enough to somehow enforce the no-signalling condition, i.e. to ensure that no communication is possible between the measurement devices from the moment the input is selected to the moment the output is displayed and recorded. Simultaneity provides a way to derive the no-signalling condition from the laws of relativistic physics, but simpler approaches can be used in practice.
The following table shows the probability distribution for the four possible joint output pairs $(o_A, o_B)$, conditional to the four possible joint input pairs $(i_A, i_B)$:
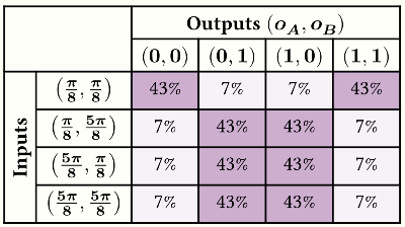
Note how the outputs of this protocol are random, but correlated. Each of these two elements plays a specific role in contextual cryptography: the correlation patterns are exploited to implement classical cryptographic primitives, while the randomness provides the source for their security.
The conditional probability distribution generated by this experiment is contextual: it is possible to show that ~42% of the randomness is intrinsic, i.e. it cannot be predicted as a function of local input choices when the no-signalling condition is enforced. We will show how to compute this number, known as the contextual fraction, in a future post.
As long as we can find interesting cryptographic applications for our correlation patterns, the unpredictability afforded by contextuality can be distilled into cryptographic security. To formulate one such interesting application, we consider a slightly more complex scenario, known as Mermin’s GHZ experiment.
Mermin’s GHZ Experiment
Three parties — call them Alice, Bob and Charlie — each have one of three qubits in an entangled state $\vert\text{GHZ}_3\rangle$, as shown by the following circuit:
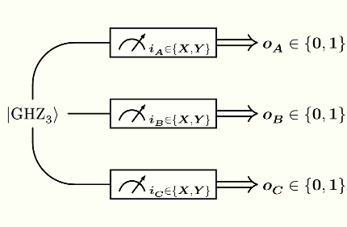
Alice, Bob and Charlie are free to measure their qubits in the X or Y basis. The inputs for this protocol are again the measurement choices: they are binary, taking values $i_A, i_B, i_C \in \lbrace X, Y\rbrace$. The outputs for this protocol are again the measurement outcomes: they are also binary, taking values $o_A, o_B, o_C \in \lbrace 0, 1\rbrace$ by convention.
Alice, Bob and Charlie measure their qubits, by flipping a random coin each to select their input; they do so simultaneously, or otherwise enforcing the no-signalling condition. The following table shows the probability distribution for the eight possible joint output triples $(o_A, o_B, o_C)$, conditional to a choice of four possible joint input triples $(i_A, i_B, i_C)$:
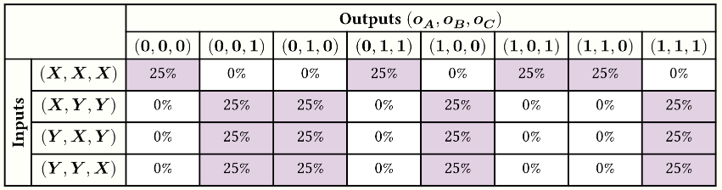
We have restricted our attention to the four input triples where an even number of parties — either none of them or exactly two of them — chooses the Y basis; the remaining four input triples produce uniformly random outputs, which are useless for cryptographic purposes.
The outputs are again random but correlated. This time, however, the correlations follow a stronger pattern: the XOR of the outputs is deterministic, as a non-trivial function of the input triple. The following table shows the probability distribution for the XOR of the outputs, conditional to our four chosen joint input triples:
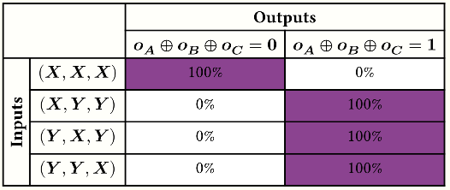
In fact, the outputs are not just random: they are as random as possible conditional to the requirement that their XOR be deterministic. The conditional probability distribution generated by this experiment is maximally contextual: it is possible to show that 100% of the randomness is intrinsic. Again, we will show how to compute this contextual fraction in a future post.
The combination of high intrinsic randomness with a deterministic correlation pattern makes the outputs produced by Mermin’s GHZ experiment especially suited for cryptographic application, namely as part of the HBB quantum secret sharing protocol.
Quantum secret sharing
In the HBB quantum secret sharing protocol, Alice wishes to share a secret with Bob and Charlie, in such a way that the secret can be revealed only when they both agree to do so. Without loss of generality, we can restrict our attention to the case where the secret consists of a single bit, since longer binary secrets can be shared by sharing their individual bits independently. The protocol has two phases: sealing and unsealing.
The sealing phase of the protocol proceeds as follows:
- Alice, Bob and Charlie perform Mermin’s GHZ experiment, selecting their inputs $i_A, i_B, i_C \in \lbrace X, Y \rbrace$ by flipping a coin each, and obtaining outputs $o_A, o_B, o_C \in \lbrace 0, 1 \rbrace$, which they keep secret.
- Bob and Charlie announce their inputs publicly to Alice.
- If the three inputs don’t have an even number of Y measurement choices, Alice announces publicly that the round is void, and the protocol restarts from step 1 (using another GHZ state). Otherwise, she computes a correction bit $k := o_A \oplus o_B \oplus o_C$ based on the three inputs $i_A, i_B, i_C$ now in her possession.
- Alice XORs the secret bit $x_A$ with the correction bit $k$ and her output $o_A$, announcing the resulting encrypted secret $s := x_A \oplus k \oplus o_A$, which is uniformly random to either one of Bob and Charlie individually.
The following picture depicts the sealing phase in its entirety, in the case where the round is not void:
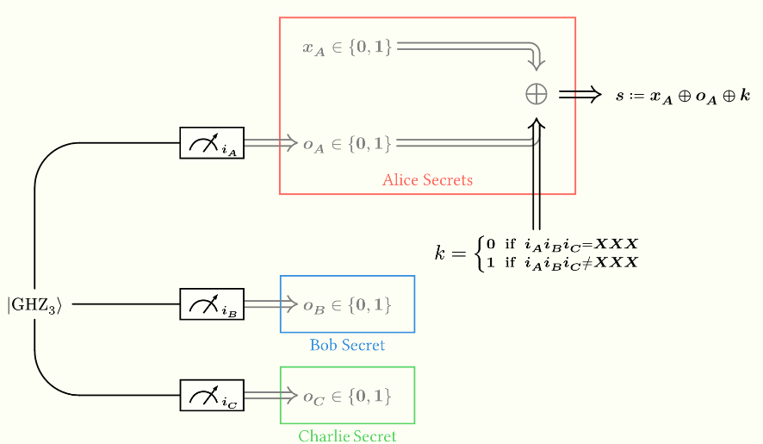
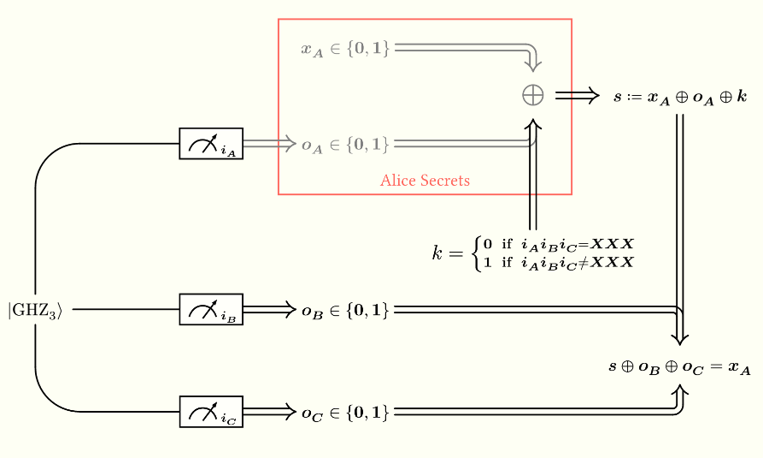
Bob and Charlie manifest their agreement to unseal the secret by revealing their secret bits $o_B, o_C$; this can be to each other, to a third party, or as a broadcast to the world. Any party in possession of the binary value $o_B \oplus o_C$ can then unseal the secret as follows:
\[s \oplus o_B \oplus o_C = x_A \oplus k \oplus o_A \oplus o_B \oplus o_C = x_A\]The following picture depicts the full protocol, inclusive of both the sealing and the unsealing phases:
Coming Next
In this post, we have introduced some of the fundamental ideas behind contextual cryptography, at a high level and with a view to drafting a concrete pipeline for the design of novel cryptographic protocols. In coming posts, we will dive deeper into the mathematical technicalities of contextuality:
- Bell’s Theorem
- Mermin’s Contextuality Argument
- Mathematics of Contextuality I - Causally Flat Scenarios
- Mathematics of Contextuality II - Causally Static Scenarios
- Mathematics of Contextuality III - Causally Dynamic Scenarios