How do we guarantee secrecy for key-exchange protocols? Ask a quantum information theorist and the answer comes quickly: by using non-locality. The idea is straightforward: quantum mechanics offers a new account of randomness. It can generate behaviours that are intrinsically random and, crucially, incompatible with any causal-deterministic explanation. There is therefore the possibility of producing correlations that cannot, in principle, be correlated with any third party.
As a consequence, quantum cryptography allows us to reproduce correlations that are provably secret: any deterministic knowledge about them, leaked to a third party, would amount to an impossible explanation.
This story has been formalised and studied at length in the literature on device-independent quantum key distribution (DIQKD). We will soon publish a broader overview of the state of the art in this important topic of quantum information theory. Today, however, we comment on a question posed — and answered — in a 2021 work by Máté Farkas and collaborators, titled: Bell nonlocality is not sufficient for the security of standard device independent quantum key distribution protocols.
This paper is often cited to debunk one of our core working principles at NeverLocal: the equivalence between secrecy and non-locality (or, more generally, contextuality). I will instead argue that the work, when carefully read, points to a different conclusion — one that can be instead used to corroborate our intuition.
Imagine, for the sake of argument, that you and a friend want to share a secret key. Suppose you have a magical device that generates random bits according to the following conditional probabilities. Inputs $x,y\in \lbrace 0,1\rbrace$, outputs $a,b\in \lbrace 0,1\rbrace$, with the defining relation $a\oplus b = x\cdot y$. Each allowed output has probability $1/2$; disallowed outputs have probability $0$.
This is the Popescu–Rohrlich (PR) box. We are talking about a hypothetical device: PR boxes combine strong correlations with free choice of inputs in a way that, while non-signalling, can neither be realised classically nor quantum mechanically. There are good reasons for this: the existence of PR boxes would trivialise communication complexity. We need not dwell on that further, but it’s a fascinating topic.
For the sake of simplifying our argument, we start by hypothesising the existence of such a device. The outputs are perfectly correlated except when both agents choose input $1$, which yields perfect anti-correlation. Flipping one party’s bit in that case restores perfect agreement, so a perfect key is within reach. But the real magic lies in the extremality of the correlations, as we now define it. Let $p_{\mathrm{PR}}(a,b\mid x,y)$ be the conditional distribution. Extremality means that if we try to decompose the conditional distribution as a convex combination of two no-signalling conditional distributions $p_1$ and $p_2$, in the form
\[p_{\mathrm{PR}}(a,b\mid x,y)=\alpha\,p_1(a,b\mid x,y)+(1-\alpha)\,p_2(a,b\mid x,y),\]for some $\alpha \in [0, 1]$, then we necessarily have that $p_1=p_2=p_{\mathrm{PR}}$, i.e. the decomposition is trivial. Thinking geometrically, we say that the PR box is a (non-deterministic) vertex of the no-signalling polytope.
Now consider a no-signalling eavesdropper, Eve, with a tripartite distribution $p(a,b,e\mid x,y,z)$ whose marginal reproduces the observed correlations, in the form
\[p(a,b\mid x,y)=\sum_{e} p(a,b,e\mid x,y,z)=\sum_{e} p(e\mid z)\,p(a,b\mid x,y,z,e),\]where Eve’s output $e$ is independent of the inputs $x$ and $y$ of Alice and Bob, i.e. there is no signalling to Eve. We also assume i.i.d. rounds. Fixing Eve’s input $z$, extremality forces
\[p(a,b\mid x,y,z,e)=p_{\mathrm{PR}}(a,b\mid x,y)\]for all possible values $e$ of Eve’s output, and as a consequence we get that
\[p(a,b,e\mid x,y,z)=p_{\mathrm{PR}}(a,b\mid x,y)\,p_E(e\mid z)\]Eve’s knowledge $e$ in each round is independent of the outputs $a$ and $b$ of Alice and Bob. This yields a perfectly secure protocol: it suffices for one party to reveal which measurement was used so that, in the rounds where they have both chosen $1$, one of them can flip their bit and recover a perfect correlation.
Strikingly, in the extremal, non-physical case of PR boxes, even revealing both measurement choices does not help Eve: at best, she learns whether the raw bits were correlated or anti-correlated, but she still knows nothing about their actual values. Some information about the context must be made public, but it needn’t be the entire context nor both parties’ choices.
Let us turn to a more realistic case. Consider a two-qubit Werner state, defined to be a mixture of a maximally entangled Bell state and white noise:
\[\rho^{v}=v\,\lvert\phi^+\rangle\langle\phi^+\rvert+(1-v)\,\mathbb{1}/4.\](Equivalently, one could take the singlet $\lvert\psi^-\rangle$; these two formulations are related by local unitaries and don’t essentially change the argument.) As $v$ varies, measuring $\rho^{v}$ with fixed projective observables traces a line from the maximally non-local quantum point (closest to the PR box) toward the centre of the no-signalling polytope (the uniform mixture of deterministic behaviours).
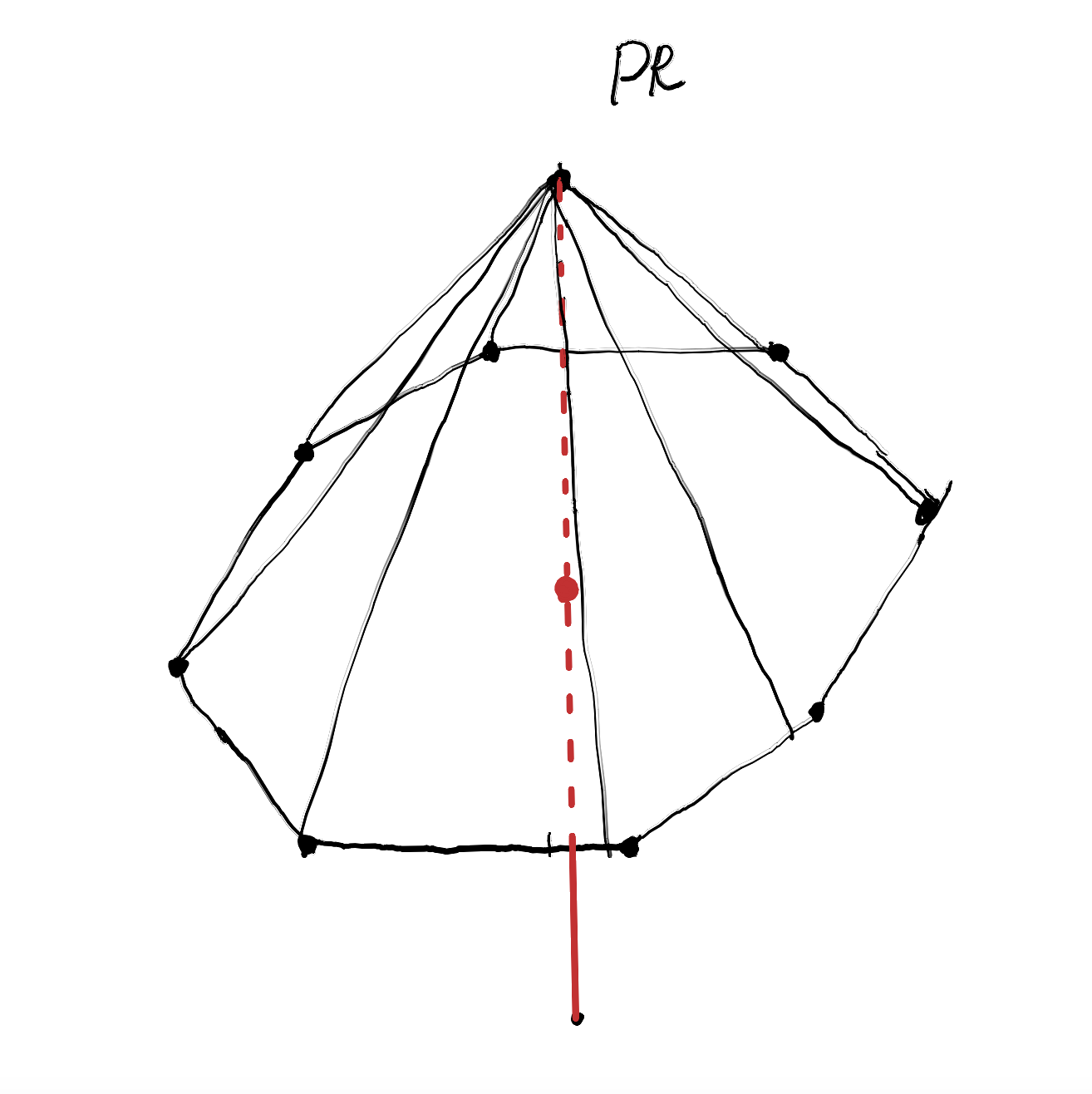
It is known that for visibilities $v\le v_{\mathcal L}^{\,w}\approx 0.6829$ the two-qubit Werner state admits a local hidden-variable model for all projective measurements (cf. Hirsch et al., 2017), whereas for $v\gtrsim 0.6964$ there exist projective measurements that yield non-local correlations (cf. Diviánszky et al., 2017). The previously referenced paper of Farkas et al., 2021 shows that there are Werner states exhibiting non-locality which are nevertheless useless for key generation, at least in the common DIQKD setting where both parties later announce their inputs. Non-locality is clearly necessary to set in motion the mechanism we discussed — the verifiable, fundamental randomness of quantum correlations — but, the paper claims, might not be always sufficient when the protocol publicly reveals the entire context.
Here are the specifics of the attack they describe. Eve prepares, with some probability $q_{\mathcal L}^{\,w}$, a local device that simulates the correlations of $\rho^{v_{\mathcal L}^{\,w}}$ under the chosen projective measurements; otherwise she prepares a non-local device simulating the correlations of the unit-visibility state ($v=1$) under the same measurements. Linearity fixes
\[q_{\mathcal L}^{\,w}=\frac{1-v}{1-v_{\mathcal L}^{\,w}}.\]Each component is no-signalling, and Eve knows which component is used each round. When the device is local, Eve’s output is maximally correlated with Alice’s and Bob’s outputs; when it is non-local, Eve has no information.
Writing $e \in \lbrace 0, 1, 2 \rbrace$ for Eve’s output, the setting we describes results in the following decomposition:
\[p_{ABE}(a,b,e\mid x,y) = \begin{cases} q_{\mathcal L}^{\,w}\,p_{AB}^{\,v=v_{\mathcal L}^{\,w}}(a,b\mid x,y) & \text{ when } a = b = e\\ q_{\mathcal L}^{\,w}\,p_{AB}^{\,v=v_{\mathcal L}^{\,w}}(a,b\mid x,y) & \text{ when } a \neq b \text{ and } e = 2\\ \big(1-q_{\mathcal L}^{\,w}\big)\,p_{AB}^{\,v=1}(a,b\mid x,y) & \text{ when } a = b \text{ and } e = 2 \\ 0 & \text{ otherwise } \end{cases}\]Remember that the authors assume here that Alice and Bob will publicly announce the values of their inputs $x$ and $y$ after locally choosing them. When $e=a\in \lbrace 0,1\rbrace$, the pair is deterministic (no secrecy left to distil); when $e=2$, the mixture of the “uncorrelated slice” of the local box with the non-local slice is arranged so that Alice’s and Bob’s bits have the distribution of two independent fair coins in every context. Thus the conditional mutual information $I(A:B\mid E)$ always vanishes — where $A$, $B$ and $E$ are the (correlated) random variables for the outcomes $a$, $b$ and $e$ of Alice, Bob and Eve, respectively. Additionally, we can define the intrinsic information as the minimum of conditional mutual information over all possible post-processing $\Phi: E_{raw} \rightarrow E$ applied by Eve to her raw output $E_{raw}$ to obtain her final output $E$:
\[I(A,B\downarrow E):=\min_{\Phi} I(A\!:\!B\mid E_{raw}),\]One of the possible post-processing functions $\Phi$ that Eve can apply is the one described in the conditional distribution decomposition above, implying that the intrinsic information $I(A,B\downarrow E)$ is zero. Since the intrinsic information provides an upper bound to the asymptotic key rate, we conclude that the the key rate also vanishes in this construction.
So, does this mean that these non-local correlations cannot be used to extract a secure key? Probably not. The argument collapses once we relax the assumption that the entire context $(x,y)$ is published. Recall the PR-box idealisation: revealing a single party’s input sufficed for reconciliation without leaking the value of the raw bit. CHSH-type protocols rest on the same intuition. Can we reconstruct a key by publishing only one input and leaving the global context underdetermined?
For the Werner noise model, this idea already appears in the classic paper by Antonio Acín, Nicolas Gisin, and Lluis Masanes, titled From Bell’s Theorem to Secure Quantum Key Distribution. They show that, against individual no-signalling attacks and with appropriate reconciliation, any Bell-violating correlations have positive intrinsic information, suggesting that with one-sided disclosure the intrinsic information remains positive throughout the non-local regime. While their analysis considers a specific attack model, one can generalise to arbitrary convex-combination attacks; we will present the details elsewhere.
There are different flavours of non-locality, and it is misleading to compress the “quantum fingerprint” of correlations into a single number. Different non-local behaviours call for different DIQKD protocols to reveal and harness their inherent secrecy. This is the core of our technology vision at NeverLocal: to systematically exploit all possible shapes of non-locality to generate a whole zoo of interesting cryptographic protocols. Much more on this to come.