A Greenberg-Horne-Zeilinger (GHZ) state is an entangled quantum state that serves as a resource, as the “quantum spice”, in many celebrated cryptographic protocols, including quantum secret sharing. This state is the source of a particularly strong form of non-locality. In this post, we will explain the power and meaning of the correlations that can be obtained by measuring this quantum resource. It is perhaps the simplest way to understand Quantum theory’s conceptual departure from classicality, while also providing the quantitatively strongest evidence of the breakdown of classical intuition. Two birds with one stone.
While pinpointing the computational advantage of quantum algorithms is a difficult task—one that requires careful framing of the resources at play—the advantage of using quantum resources in communication protocols becomes glaringly obvious. Communication protocols are defined by their adherence to a particular causal structure. Thus, while “quantum supremacy” remains a highly debated topic and represents the holy grail of quantum computation (arguably achieved only recently), the reality is that even the simplest experiments in quantum foundations already showcase an advantage from using quantum resources. This advantage, however, is conditional on adhering to specific causal assumptions which is not usually a concern of the study of the complexity of algorithms; it is nevertheless one of the most fundamental and natural assumption in communication-theoretical settings.
The GHZ State
Recall that in quantum theory, the full description of a physical state is given by a normalized vector living in a complex Hilbert space (we do not worry if these words don’t mean anything to the reader). As such, we can take the linear superposition of them without leaving the realms of the theory. We can define the GHZ state as the equally weighted superposition of two states in the computational basis, $\mid 000\rangle$ and $\mid 111\rangle$:
\[\mid \text{GHZ}\rangle = \frac{1}{\sqrt{2}} \left( \mid 000\rangle + \mid 111\rangle \right).\]Where $\mid 111 \rangle$ and $\mid 000 \rangle$ are shortcuts for respectively $\mid 1 \rangle \otimes \mid 1 \rangle \otimes \mid 1 \rangle$ and $\mid 0 \rangle \otimes \mid 0 \rangle \otimes \mid 0 \rangle$: correspond to three independent and simultaneous preparation of the same $\mid 0 \rangle$ and $\mid 1 \rangle$, two orthogonal states, i.e., maximally distinguishable. Other than that the association of $\mid 0\rangle$ and $\mid 1 \rangle$ to a specific physical configuration is arbitrary. For example, for superconducting architectures using Transmon qubits, they usually correspond to the ground and first excited states of a nonlinear oscillator formed by a Josephson junction and a capacitor, but other technologies and other ways to understand these conventional ‘computational states’ are widespread.
This seemingly innocuous quantum state represents a type of maximally entangled state, just like the Bell state. Unlike the two-qubit case, where the maximally entangled state is essentially unique, there are different classes of ‘maximal’ entanglement for three or more qubits that cannot be interconverted by local operations. For example, the following $W$ state represents a different class of maximal entanglement:
\[\mid W\rangle = \frac{1}{\sqrt{3}} \left( \mid 001\rangle + \mid 010\rangle + \mid 100\rangle \right).\]One of the crucial differences between the $W$ and the $GHZ$ state is that only the latter can achieve maximally nonlocal correlations. An opportunity, once more, to underline the difference between entanglement and nonlocality. While entanglement is an algebraic property of certain quantum states, non-locality is an operational manifestation of entanglement which can be expressed fully at the level of correlations without making reference to the theory.
Note that while the GHZ state can achieve levels of non-locality impossible to achieve with a $W$ state, on the other hand, the $W$ state has the peculiar property that it’s entanglement is more robust, i.e., it remains entangled when one of the sub-system is ignored, discarded. This is not the case with the $GHZ$, which loses all the entanglement when any of its subsystem is ignored.
Quantum Secret Sharing Protocol
In a previous blog post, we briefly explained the quantum secret sharing protocol. In this protocol (introduced in 1988 by Hillery, Bužek and Berthiaume), Alice wants to share a secret with Bob and Charlie, but only if both agree to do so. The idea is to securely delocalise a secret bit, which can be recovered only when all the parties involved reunite. We will see that quantum mechanics allows us to guarantee that no-one except for the concordant parties, can be in possession of the secret.
The parties start by sharing between them a GHZ state for every secret bits that Alice is willing to share, which they can measure and manipulate from their allocated subsystems (1 qubit each). Here is a brief review of the protocol:
- Step 1: In the first stage, the three players perform measurements on the GHZ state, selecting their inputs $i_A, i_B, i_C$ from the dichotomic measurements denoted (more about this measurements later) ${X, Y}$ and, as a consequence, obtain outputs $o_A, o_B, o_C$, which they keep secret.
The reader does not need to know the details of the theory of quantum measurements: for the experience reader we could have said that $X$ and $Y$ are specific hermitian operators, i.e., classes of linear maps which are in a one-to-one correspondence with the so-called projective measurements; procedures to sharply measure a quantum state. Specifically $X$ and $Y$ refer to the Pauli matrices $X = \sigma_x$, $Y = \sigma_y$. For the purpose of this blog post, $X$ and $Y$ are just symbols labeling the measurements, which produce $(0,1)$-valued outcomes probabilistically.
-
Step 2: Bob and Charlie publicly announce their inputs, which Alice uses to either abort the protocol—when the number of $Y$ measurements is odd (e.g., $XXY$)—or to compute a correction bit $k$ when the total number of $Y$ measurements is even:
\[k = \begin{cases} 0 & \text{if } i_A i_B i_C = X X X, \\ & \text{if } i_A i_B i_C \neq X X X. \end{cases}\] -
Step 3: Alice XORs the secret bit $x_A$ with the correction bit $k$ and announces the encrypted secret $s := x_A \oplus k \oplus o_A$. The encrypted secret appears completely random to both Bob and Charlie. However, if both agree to reveal the secret, they can use their outcomes to compute:
\[s \oplus o_B \oplus o_C = x_A \oplus k \oplus o_A \oplus o_B \oplus o_C.\]
This will reveal the original secret bit possessed by Alice, but we postpone a detailed explanation of why that is the case for later.
We will not delve into an explanation about how quantum mechanics assigns outcome probabilities to measurements. This is part of the linear algebraic structure of the theory, often a source of confusion when one is starting to understand the consequences of the theory. It suffices to say that by virtue of the algebraic structure of $\mid GHZ \rangle$, the outcomes observed by the three agents are probabilistic, fundamentally probabilistic. The following table fully describes the way the agents interact with this quantum resource:
Each player has two choices of measurement; as they are free to perform their measurement choice simultaneously we can assume they are spacelike separated—i.e., no signal travels from one player to another at the moment they choose their measurement.
We note that the conditional probability table shown above is compatible with this no-signalling assumption. For example, if we ignore Alice’s outcome by marginalizing over her bit (e.g., by identifying the events $(0,0,1)$ and $(1,0,1)$ and summing their respective probabilities), we obtain the following table representing the marginal behaviour:
We see that, independently of Alice’s choice to measure $X$ or $Y$ (the two different shades of blue in the table), the outcomes for Bob and Charlie occur with the same probabilities. Moreover, the outcomes are all equally likely and unbiased with respect to the measurement choices. Due to the symmetry of the table, this holds when marginalizing over any subset of the three agents.
Returning to the original table, the rows highlighted in red represent the situations where Alice aborts the protocol. These are precisely the measurement contexts that give rise to a totally mixed probability distribution, lacking any interesting structure that can be exploited. On the other hand, if we focus on the contexts indexed by an even number of $Y$ measurements, we see that the outcomes satisfy the following relationship:
Despite the outcomes being random—maximally random for any subset of agents—when considering the distribution of all three outcomes, we notice that the context $XXX$ deterministically induces an even number of $1$s, while all other contexts always produce an odd number. The outcomes, which appear random locally, hide a strong regularity when all three parties are considered together.
Returning to the protocol, when both Bob and Charlie decide to reveal the secret, they use their outcomes to compute:
\[s \oplus o_B \oplus o_C = x_A \oplus k \oplus o_A \oplus o_B \oplus o_C.\]We can read from the table that $o_A \oplus o_B \oplus o_C = k$, and therefore:
\[s \oplus o_B \oplus o_C = x_A \oplus k \oplus k = x_A.\]The bit $k$ is the correction that takes care of the fact that the sum modulo two of the outcomes can depend on the choice of measurement context. Alice has complete information about the broadcasted measurement choices. Despite not knowing the individual values of the outcomes, she knows with certainty what the sum of the values modulo $2$ will be.
Nonlocality and PR-Boxes
The protocol is striking in its simplicity, and at first glance, it might be difficult to see anything quantum-mechanical happening. One reason is that “local” behaviour is so ubiquitous in nature that we lack the intuition to distinguish it from nonlocal behaviour. But table of conditional proabbility distribution that looks absolutly innocuous to the untrained classical eyes may reveal some very counterintuitive properties. For example, the following table showcases the simplest and most paradigmetic form of nonlocality and is known as a PR-box (from Popescu and Rohrlich):
Alice and Bob (in this case, limited to two players) choose to perform a measurement labeled $0$ or $1$ each round. What they observe is that the outcomes are always correlated, except when both choose measurement $1$, which toggles an anticorrelation of the outcomes.
Suppose this stochastic behaviour arises from an underlying deterministic mechanism, obfuscated by some correlated exogenous variable. The mechanism would be allowed to use information determined locally by the agents but would have to do so independently, ensuring compatibility with the no-signalling hypothesis. We therefore expect the conditional correlations to depend on hidden variables $\Lambda$: a set of deterministic no-signaling behaviours equipped with a probability distribution that selects one of the available deterministic behaviours at each round.
The table above would have to be realized by averaging over these deterministic behaviours:
\[p(o_A, o_B \mid i_A, i_B) = \sum_{\lambda \in \Lambda} p(\lambda) p_\lambda(o_A, o_B \mid i_A, i_B),\]where each $p_\lambda(o_A, o_B \mid i_A, i_B)$ is a deterministic $0$-$1$ valued distribution which is local so that the output $o_A$ only depend on the input $i_A$ and mutatis mutandis for $o_B$. This function can be shown to be equivalent to selecting a definite deterministic outcome for every choice of measurement simultaneously. We can argue that such an explanation is impossible by examining a specific round where the deterministic behaviour $\lambda’$ is selected. Suppose Alice measures $i_A = 0$ and obtains the outcome $o_A = 0$. Given that the outcomes are perfectly correlated when both Alice and Bob choose $i_A = i_B = 0$ (as supported by the empirical behaviour), it follows that if Bob also measures $i_B = 0$, he must observe the outcome $o_B = 0$.
Now, keeping the deterministic behaviour $\lambda’$ fixed—assuming it has been realized in this round—we can also consider a counterfactual scenario where both Alice and Bob measure $i_A = i_B = 1$. In this case, the deterministic behaviour $\lambda’$ would require both outcomes to be $0$. However, the probabilistic behaviour, as described in the second and third columns, dictates that the outcome for $i_A = 1$ must be correlated with the outcome for $i_B = 0$, implying that $o_A$ must be $1$ when $i_A = 1$. Similarly, for Bob’s measurement $i_B = 1$, the outcome must also be $1$ due to the same correlation with $i_A = 0$.
This leads to a contradiction: while the deterministic behaviour $\lambda’$ requires the outcomes for $i_A = i_B = 1$ to be perfectly correlated (i.e., both $0$ or both $1$), the probabilistic behaviour explicitly rules out perfect correlation in this case, as indicated by the last row. Therefore, the scenario is impossible.
Impossibility of Classical Hidden Variables
We can attempt to construct a deterministic hidden model for the quantum secret sharing protocol, we find that a classical explanation is similarly impossible.
Suppose that at a given round, a deterministic behaviour assigns outcomes for every local measurement that the three agents sharing a GHZ state can perform. Let $a, b, c$ be the predetermined outcomes for the $X$ measurements, and let $a’, b’, c’$ be the outcomes for the $Y$ measurements. From the parity arguments developed earlier, we see that the values must satisfy the following constraints:
\[\begin{align*} a \oplus b \oplus c &= 1, \\ a \oplus b' \oplus c' &= 0, \\ a' \oplus b \oplus c' &= 0, \\ a' \oplus b' \oplus c &= 0. \end{align*}\]Adding these four constraints modulo $2$:
\[(a \oplus b \oplus c) \oplus (a \oplus b' \oplus c') \oplus (a' \oplus b \oplus c') \oplus (a' \oplus b' \oplus c) = 1 \oplus 0 \oplus 0 \oplus 0.\]The terms $a, b, c, a’, b’, c’$ each appear twice in the sum. Since $x \oplus x = 0$ for any $x$, the left-hand side simplifies to the contradiction:
\[0 = 1.\]Meaning no local hidden variable (LHV) model can satisfy all four constraints simultaneously.
We have seen that the correlations of the GHZ game achieve two goals: they form a three-partite correlation that allows for the secret sharing (which boils down to the understanding that the addition modulo two of the outcomes is deterministic) but also that they do so while being maximally non-local.
We can of course think of a similar classical protocol involving $n$ parties in which they share a uniformly random string of $n$-bits among the ones satisfying:
\[x_0 \oplus x_1 \oplus x_2 \oplus x_3 \ldots \oplus_n = k\]Alice’s secret $s \oplus x_A$ will similarly be unveiled only when there is agreement among all parties. The crucial difference is that using a GHZ state allows one to do this in a way that is provably secure. And no, this security does not come from the no-cloning principle or from a handwavy appeal to Heisenberg uncertainty. The security is independent of the underlying theory that reproduced the correlations; it is ingrained in the conditional probability distribution. It is this apparent flaw of the protocol, the fact that a correction is needed for only one of the contexts, that actually guarantees that there cannot be a malicious actor preparing the randomness that is used to make Alice’s secret distributed but secure, fundamentally delocalizing the responsibility of its reveal.
If we believe such a malicious agent to exist—one that knows the value of every measurement preemptively—then we get into a logical contradiction at any round of the protocol. Any use of the GHZ state to construct the string will defy the support of the table obtained by using quantum resources.
We do not need to have the faith that GHZ states are shared between the parties and conclude that properties of the theory protect the secrecy of the correlations, it is an empirical fact independent from the device and the inener workings of a specific theory. If a sufficiently large number of bits is reproduced and the distribution approximates the table of the GHZ distribution, then one knows that the secret cannot be known to a malicious party.
In order to make this novel type of security work, contextuality (known as non-locality when the overarching assumption is a strictly causal one) is always a crucial ingredient. It has two embodiments: one qualitative, i.e, the realization that physical systems subsume different ways of accessing them and it might be impossible—even in principle—to think of assigning to this different classical perspective on the object a definite value. And one quantitative, which is subsumed by the calculation of the local/contextual fraction.
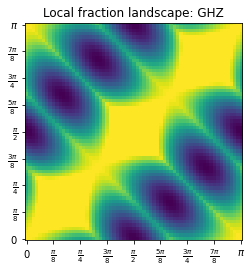
To visualize non-locality quantitatively, we can plot the non-local fraction with respect to the specific choices of measurements. The $X$ and $Y$ measurements both correspond to particular projective measurements with respect to the two following axes:
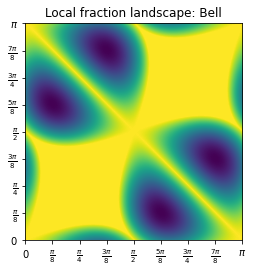
Using the same formalism of the post on Bell non-locality and the post on bell-nonlocality with multiple settings, the projective measurements $X,Y$ would correspond to measurements with respect to the equatorial angles $\phi_0 = 0, \phi_i = \frac{\pi}{2}$. Note that if we measured a Bell state choosing between the $X$ and the $Y$ measurement, we do not observe any non-locality:
For a GHZ state, the probability of observing the outcomes $o_A,o_B,o_C$ given the measurement choices identified by the equatorial angles $\theta_A, \theta_B, \theta_C$ is given by:
\[P(o_a, o_b, o_c \mid \theta_a, \theta_b, \theta_c) = \frac{1 + (-1)^{o_a + o_b + o_c} \cos(\theta_a + \theta_b + \theta_c)}{8}\]If we calculate the same local fraction for the GHZ state, we observe that we reach a peak of nonlocality (maximal as the local fraction vanishes completely) precisely at $\phi_0 = 0$: